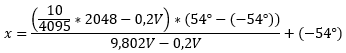Skalierung von (Analog-) Werten

[oliver.tonn]

Zuviel Werbung?
-> Hier kostenlos registrieren

Kapitelübersicht der FAQ
​

Kapitel 1 (Einführung)
Kapitel 2 (Begriffsdefinition)
Kapitel 3 (Genauere Erläuterung anhand von Beispielen)
Kapitel 4 (Erläuterung der verschiedenen Auflösungen und Darstellungsformen analoger Eingangswerte)
Kapitel 5 (Umsetzung von Skalierungen in SPS-Programme)
Kapitel 6 (Tipps für Steuerungen ohne Fließkomma Unterstützung)

 

[oliver.tonn]

Einführung
Bei verschiedenen SPS-Projekten ist es erforderlich Werte eines Bereichs in einen anderen umzurechnen, dies wird auch skalieren genannt.
Der Grund hierfür kann sein, dass eine analoge Eingangskarte den digitalisierte Wert nicht selber in die physikalische Größe wieder umrechnet, oder eine dezentrale Peripherie (z.B. FU, Heizregler, usw.) liefert verschiedene Größen (z.B. Strom, Spannung, Leistung, usw.) lediglich in Form einer nichtssagenden Integerzahl. In solchen Fällen muss der Eingangswert skaliert werden, um einen Wert in die physikalische Größe umzurechnen.
Dieser FAQ Beitrag soll möglichst umfangreich aufzeigen, wie dies geht und was alles dabei zu beachten ist. Eine kompaktere Variante ist im Thread
"Skalierung von (Analog-) Werten (Kompakt)" zu finden. Dieser Beitrag ist so weit wie möglich Steuerungsunabhängig, sollte es jedoch Besonderheiten bei bestimmten Steuerungen geben wird dies entsprechend erwähnt.
Alle hier aufgeführten Beispiele setzen voraus, dass die entsprechend genutzte Steuerung Fließkommazahlen verarbeiten kann. Einige sogenannte Kompaktsteuerungen können jedoch keine Fließkommazahlen verarbeiten, im Kapitel "Tipps für Steuerungen ohne Fließkomma Unterstützung" wird beschrieben und anhand von Beispielen gezeigt, wie man trotz dieses Mankos Skalierungen mit einer gewissen Genauigkeit realisieren kann.

 

[oliver.tonn]

Zuviel Werbung?
-> Hier kostenlos registrieren

Begriffsdefinition
Bevor es ans Eingemachte geht, hier zunächst eine kurze Erklärung der in dieser FAQ verwendeten Begriffe.
Der zu messende Wert (z.B. Temperatur, Position, usw.) wird in dieser FAQ als physikalische Größe bezeichnet, falls neben der analogen Eingangskarte auch ein Messwandler verwendet wird, wird dessen Ausgangssignal als Einheitssignal bezeichnet und der digitalisierte Wert den die analoge Eingangskarte oder die dezentrale Peripherie an die SPS übermittelt heißt in dieser FAQ Digits oder Eingangswert.

 

[oliver.tonn]

Genauere Erläuterung anhand von Beispielen
Das Grundprinzip einer Skalierung ist ein Dreisatz, wobei auf der einen Seite des Gleichheitszeichen die Digits stehen und auf der anderen die Werte in der physikalischen Größe. Soweit die Bereiche (Minimaler physikalischer Wert - maximaler physikalischer Wert, minimaler Wert der Digits - maximaler Wert der Digits) auf beiden Seiten jeweils ein bei 0 beginnender oder ein um den Nullpunkt symmetrisch verlaufender Bereich ist, gestaltet sich der Dreisatz relativ einfach, da nicht wirklich viel beachtet werden muss. Letzten Endes wird über diesen Dreisatz ausgerechnet, was für einen Sprung der physikalischen Größe eine Änderung bei den Digits um ein Bit zur Folge hat. Das Ergebnis wird dann mit dem Messwert multipliziert. Folgende Zahlenwerte werden in der Gleichung verwendet:

- Digits des analogen Eingangs
- Bereich der Digits des analogen Eingangs (Bei Bereichen die bei 0 beginnen oder sich symmetrisch um 0 bewegen ist dies meist die größte darstellbare Zahl)
- Bereich der physikalischen Größe (z.B. bei 0-100% = 100)
- Istwert der physikalischen Größe

Hier mal die Formel des Dreisatzes:

Ich habe beim Bereich der Digits geschrieben, dass hier die größte darstellbare Zahl eingetragen werden muss, dies trifft aber nicht auf alle Hersteller zu. Bei Siemens zum Beispiel ist dies anders, hier wird nicht die größte darstellbare Zahl verwendet, sondern 27648. In diesem Fall muss diese Zahl eingetragen werden.
Als nächstes wird die Formel mal mit Leben gefüllt (1000 = Digits des analogen Eingangs, 10000 = Bereich Digits, 10 = Istwert physikalische Größe, 100 = Bereich der physikalischen Größe):

Da der Istwert der physikalischen Größe nicht bekannt ist, dieser soll ja schließlich durch den Dreisatz berechnet werden, wird stattdessen eine Variable (x) eingesetzt.
In diesem Kapitel wird immer der je nach Auflösung höchste Wert der Digits für die Berechnung genutzt. Es gibt Hersteller, z.B. Siemens oder Beckhoff, die unabhängig von der Auflösung immer mit einem gleich hohen Wert arbeiten. Auf diesen Umstand, die verschiedenen Auflösungen und die Varianten für die Art der Darstellung der analogen Messwerte wird im Kapitel "Erläuterung der verschiedenen Auflösungen und Darstellungsformen analoger Eingangswerte" näher eingegangen.

 

[oliver.tonn]

Hier nun ein erstes einfaches Beispiel, dass zunächst kurz Beschrieben werden soll. Ein FU (Frequenzumrichter) liefert an eine analoge Eingangsklemme eine Spannung von 0-10V, die der Drehzahl eines Motors von 0 - 1000 U/Min entspricht. Der maximal mögliche Wert den die Eingangskarte an die SPS meldet ist 32767, der an die SPS gemeldete Wert Wert beträgt 16383Dez. Die Formel sieht also wie folgt aus:

Da wir ja x als Ergebnis haben wollen muss die Formel noch umgestellt werden und sieht danach so aus:

Das Ergebnis ist rund 500U/Min.

Soweit sich beide Bereiche, sowohl der Bereich der physikalischen Größe als auch der Bereich der Digits symmetrisch um 0 bewegt funktioniert die Formel auch mit negativen Digits, dann würde die Größe des Bereichs der physikalischen Größe auch nur von 0 aus in positive Richtung angegeben werden. Der Bereich der physikalischen Größe beginnt bei diesem Beispiel bei -1000 U/Min und endet bei 1000 U/Min, hätte also eigentlich eine Größe von 2000 U/Min, es muss aber, wie schon erwähnt, in diesem Fall nur 1000 U/Min angegeben werden. Hier mal die gleiche Formel mit einem negativen Messwert:

Hier ist dann das Ergebnis rund -500U/Min.

Würden sich die beiden Bereiche (Physikalische Größe und Digits) immer nur von 0 in eine Richtung bewegen, also nur in die positive oder negative Richtung oder sich symmetrisch um 0 (z.B. -100°C - 100°C und -32767 - 32767) bewegen wäre dieser FAQ-Beitrag, was die genauere Erklärung angeht, schon zu Ende, da dem jedoch nicht so ist, geht es hier erst richtig los.
Beim nächsten Beispiel soll eine Temperatur mit einem PT100-Fühler gemessen werden, hierbei handelt es sich um einen temperaturempfindlichen Widerstand aus Platin, der bei 0°C einen Widerstand von 100Ohm hat. Dieser Messfühler ist an einen Messwandle angeschlossen, der Temperaturen von -20°C - 50°C als Einheitssignal eine Spannung von 0-10V ausgibt. Diese Spannung wird an einen Analogeingang gegeben, dessen Maximalwert 4095 beträgt. Bei diesem Beispiel ist jetzt die Besonderheit, dass sich der Bereich der physikalischen Größe (-20°C - 50°C) nicht mehr symmetrisch um 0 bewegt und die Werte der Digits nur positiv sind, so dass die Formel modifiziert werden muss. Um zu zeigen was passiert, wenn die Formel nicht modifiziert wird, erfolgt hier zunächst eine Berechnung mit der nicht modifizierten Formel. Die Werte der Digits gehen von 0 bis 4095, der Bereich der physikalischen Größe beginnt, wie erwähnt, bei -20°C und geht bis 50°C, hat also einen Bereich von 50°C - (-20°C) = 70°C und der digitalisierte Wert der Analogkarte beträgt 2340Dez. Nachdem die Werte in die Formel eingetragen wurden sähe diese so aus:

Als Ergebnis käme 40°C heraus, was jedoch falsch ist. Was lief hier verkehrt? Der Bereich der physikalischen Größe ist zwar tatsächlich 70°C, nur beginnt der Messbereich nicht mehr bei 0°C, sondern es gibt einen Offset gegenüber dem Nullpunkt von -20°C, also eine lineare Verschiebung. Da der Bereich der physikalischen Größe nicht symmetrisch ist, muss der Offset berücksichtigt und zum Ergebnis der Rechnung dazu addiert werden. Bezogen auf dieses Beispiel sehe die Formel nun so aus:

Das so ermittelte (nun richtige) Ergebnis ist 20°C.

 

[oliver.tonn]

Zuviel Werbung?
-> Hier kostenlos registrieren

Ein weiterer Stolperstein lauert, wenn der Wert der Digits nicht bei 0 beginnt. Dies kann z.B. der Fall sein, wenn man einen Sensor oder Messwandler benutzt, der 4-20mA liefert, in Fall des Messwandlers wäre die sein Einheitssignal, an einen analogen Eingang anschließt der von 0-20mA misst. In diesem Fall würde mindestens immer ein Strom von 4mA fließen den man an entsprechender Stelle rausrechnen muss. Um das folgende Beispiel nicht unnötig kompliziert zu machen beginnt der Bereich der physikalischen Größe bei 0°C und verläuft in positive Richtung und auch der Bereich der Digits beginnt bei 0 und verläuft in positive Richtung. Bei diesem Beispiel wird ein PT100 an einen Messwandler angeschlossen der Temperaturen von 0° - 100° misst und einen Strom von 4-20mA ausgibt, der analoge Eingang hat wieder einen Maximalwert von 4095 und der aktuelle Messwert beträgt 2457Dez. Wie erwähnt fließen bei dem verwendeten Messwandler mindestens 4 mA, daher müssen wir zunächst ausrechnen, welchem Digitswert der Einheitswert 4mA entspricht, dafür teilt man 4mA durch 20mA und multipliziert das Ergebnis mit dem maximalen Wert der Digits. Hier die dazugehörige Formel:

Als Ergebnis erhält man 819. Nun errechnet man die gemessene Temperatur, wobei man in der Formel vom Messwert der analogen Eingangskarte als auch vom Maximalwert der Digits die 819 abziehen muss.
Doch warum ist das so? Diesen Umstand werde ich hier kurz erklären. Wie schon erwähnt kann der analoge Eingang Ströme von 0-20mA messen, der Messwandler gibt für seinen Messbereich jedoch bekanntermaßen 4-20mA aus. Das hat zur Folge, dass selbst bei einem Messwert von 0°C ein Strom von 4mA fließt. Würde man diesen Umstand in der Formel nicht berücksichtigen, würde statt 0°C eine Temperatur von 20°C errechnet werden. Gleichzeitig beträgt der Messbereich des Stroms nicht 20mA (20mA - 0mA), sondern lediglich 16mA (20mA - 4mA), was bedeutet, dass eine kleinere Stromdifferenz vorliegen muss, damit sich der Eingangswert um ein Bit erhöht. Die Formel für dieses Beispiel sieht wie folgt aus:

Und das Ergebnis ist 50°C.

Hier kommt nun ein etwas komplizierteres Beispiel. Ein Servo, beispielsweise ein Modellbau-Servo, hat zwei (einstellbare) Endlagen, diese Endlagen liegen symmetrisch um 0° (z.B. bei +/-45°). Der Servo gibt seine aktuelle Position als Spannungssignal aus, dessen Verlauf zwar linear ist, die Endwerte jedoch nicht genau feststehen. Die Spannung wird mit einer analogen Eingangskarte gemessen, die Spannungen von 0-10V mit einem Maximalwert von 4095 liefert. Der Servo wurde nun auf einen Verfahrweg von 108° (+/-54°) eingestellt. Da bei diesem Beispiel die Bereiche sowohl der physikalischen Größe (Servoposition in °) als auch der der Digits veränderlich sind und sich auch nicht mehr symmetrisch um 0 bewegen, bzw. dort beginnen, muss die Formel an mehreren Stellen erweitert werden. Soweit die Spannung nicht weiterverwendet wird reicht es hier mit dem Eingangswert der analogen Karte zu rechnen, was bei diesem Beispiel der Fall sein soll. Bei einer Kalibrierung wurde bei der minimalen Endlage (-54°) ein Wert von 82Dez gemessen, bei der maximalen Endlage ein Wert von 4014Dez, der aktuelle Messwert der Analogkarte beträgt 2048Dez. Füllt man die Formel jetzt mit den ermittelten Werten sieht das Ganze so aus:



Da es hier doch etwas komplizierter wird, möchte ich die Formel im Einzelnen kurz erläutern. Der Bereich der Digits bewegt sich in diesem Beispiel zwar vollständig im positiven Bereich (82 - 4014), fängt jedoch nicht bei 0 an, deswegen muss hier ein Offset berücksichtigt werden. Der Offset bei den Digits muss sowohl bei der Ermittlung der Bereichsgröße als auch bei der "Korrektur" des aktuellen Messwertes berücksichtigt werden. Die Berücksichtigung bei der Ermittlung der Bereichsgröße der Digits erfolgt in der abgebildeten Formel im Nenner des Bruches, hier wird der Offset von 82Dez vom maximal möglichem Wert der Digits abgezogen, der in diesem Fall nicht 4095, sondern lediglich 4014, weil das der Endposition des Servos entspricht. Die "Korrektur" des aktuellen Messwertes erfolgt im Zähler des Bruches, auch hier wird der Offset von 82Dez abgezogen (2048Dez - 82Dez). Der "korrigierte" Messwert der analogen Eingangskarte wird mit der Größe des Bereichs der zu messenden physikalischen Größe (Position in °) multipliziert, dieser Bereich wird in der zweiten Klammer im Zähler des Bruches ermittelt. Nachdem der Bruch ausgerechnet wurde muss noch der Offset der physikalischen Größe (-54°) zum errechneten Wert des Bruchs addiert werden und man hat das Ergebnis. Die aktuelle Position des Servos beträgt 0°. Die Position des Servos wurde ja durch einen internen Messwandler als Spannung ausgeben, wobei es uns bei diesem Beispiel ausreichte lediglich den digitalisierten Wert zu kennen und nicht die tatsächliche Spannung. Beim nächsten Beispiel soll jetzt jedoch mit der Spannung gearbeitet werden, ansonsten ist es jedoch gleich. Dafür muss die Formel an zwei Stellen erweitert, bzw. verändert werden. Im Nenner des Bruchs müssen die Werte in Digits gegen welche in Volt ausgetauscht werden. Bei einem Messbereich von 0-10V bei einem maximalem Wert von 4095 entspricht der Wert von 4014Dez einer Spannung von ca. 9,802V und 82Dez einer Spannung von ca. 0,200V. Im Zähler muss der aktuelle Messwert von Digits in eine Spannung umgerechnet werden und davon dann die Spannung der negativen Endlage abgezogen werden. Die so erweiterte/geänderte Formel sieht so aus:

Als Ergebnis kommt hier rund 0° raus.
Ich denke das diese Beispiele ausreichen, um die Vorgehensweise bei der Skalierung von Messwerten ausführlich zu erläutern.

 

[oliver.tonn]

Erläuterung der verschiedenen Auflösungen und Darstellungsformen analoger Eingangswerte
In diesem Kapitel der FAQ geht es um die digitalisierten Analogwerte, den Digits. Neben verschiedenen Auflösungen (z.B. 12Bit oder 16Bit) gibt es auch verschiedene Darstellungsformen und weitere Besonderheiten die hier erläutert werden sollen.
Zunächst ein paar Worte zur Auflösung der digitalisierten Analogwerte. Die für die jeweiligen Karten angegebene Bitzahl bezieht sich auf die Auflösung des verwendeten A/D-Wandlers. Eine gängige Auflösung ist zum Beispiel 12 Bit, eine andere 16 Bit.
Hier mal ein paar Beispiele für verschiedene Bitauflösungen, dem dazugehörigen Maximalwert der Digits und einer Erklärung, warum das so ist. Bei einer Auflösung von 10 Bits wäre der maximale Wert 1023, dies ergibt sich aus der Formel 2^10 - 1 (2 hoch 10 - 1). 2 hoch 10 ergibt 1024, was der Anzahl der bei 10 Bit möglichen Bitkombinationen entspricht. Hier ist die 0 aber auch dabei, weswegen von der Zahl 1 abgezogen werden muss, wo wir dann eben bei 1023 landen. Bei 12 Bit ist die Formel entsprechend 2^12 - 1, womit wir bei 4095 landen und bei 16 Bit entsprechend bei 65535 (2^16-1). Dies gilt allerdings nur für A/D-Wandler die nur positive Zahlen ausgeben. Es gibt auch A/D-Wandler, die sowohl positive, als auch negative Zahlen ausgeben, letztere dann als Zweierkomplement. Bei einer Auflösung von 12 Bit geht der Zahlenbereich dann von -2048 - 2047. Aufgrund der Verwendung des Zweierkomplements, ist der negative Bereich um 1 größer, oder kleiner, je nach Sichtweise.
Je nach Hersteller, z.B. bei Siemens oder Beckhoff, kann es sein, dass die Messwerte unabhängig von der Auflösung des A/D-Wandlers hochskaliert werden. Diese auf den ersten Blick seltsam anmutende Vorgehensweise hat den Vorteil, dass man die analoge Eingangskarte beliebig gegen eine mit einer anderen Auflösung tauschen kann ohne eine Änderung an seinem Programm vornehmen zu müssen. Wobei bei Beckhoff neben der Skalierung noch andere Dinge erfolgen, aber dazu später mehr. Diese Hochskalierung auf eine größere Bitzahl (z.B. von 12Bit auf 16Bit) bedeutet jedoch keine Erhöhung der Auflösung, auch wenn man zunächst auf den Gedanken kommen könnte. Die kleinste Wertänderung bei den Digits ist in einem solchen Fall dann nämlich nicht mehr 1Bit, sondern sie ist entsprechend höher. Bei einer Skalierung von 12 Bits nach 16 Bits wird der Wert mit 16 multipliziert, dadurch beträgt die kleinste Wertänderung jetzt 16 (1 * 2 * 2 * 2 * 2). Weiter unten in diesem Kapitel wird in einem anderen Zusammenhang nochmals erwähnt worauf hier geachtet werden muss.
Eine weitere mögliche Besonderheit bezüglich des Digit-Bereichs ist, dass einige Hersteller nicht den gesamten möglichen Bereich (z.B. 16 Bit) nutzen, sondern nur einen Teil davon. Auch hier wird sich manch einer Fragen, warum dies gemacht wird, bedeutet dies doch auf den ersten Blick eine Verringerung der Auflösung des analogen Eingangssignals. Dies ist theoretisch zwar auch richtig, ein mit 16 Bit aufgelöstes Analogsignal ist feiner abgestuft als ein mit nur 12 Bit aufgelöstes, jedoch ist die Anzahl der Bits nicht das Einzige was die mögliche Genauigkeit begrenzt. In der Doku der Karten wird auch ein Messfehler ausgewiesen, der sich meist auf den Messbereichsendwert bezieht. Dieser Messfehler ist eigentlich immer größer als der Wert um den sich die physikalische Größe ändern müsste um eine Änderung von einem Bit zu erzielen. Als Beispiel sei hier einmal die analoge Eingangskarte EL3061 von Beckhoff angeführt. Diese Karte kann Spannungen von 0-10V mit einer Auflösung von 12 Bit digitalisieren, was bei einer Änderung um ein Bit einer Spannungsdifferenz von ca. 4,9mV entspricht. Im Gegensatz dazu hat die Karte EL3161 von Beckhoff eine Auflösung von 16 Bit was einer Spannungsdifferenz ca. 0,305mV pro Bit entspricht und deutlich feiner aufgelöst wäre. Allerdings bringt einem diese höhere Auflösung ohne besondere Maßnahmen nichts, da beide Karten einen Messfehler bezogen auf den Messbereichsendwert (Jeweils 10V) von 0,30% haben, was einer möglichen Abweichung von bis zu 30mV unabhängig vom aktuellen Messwert entspricht und es somit egal wäre, welche von beiden Karten man verwenden würde. Einen Gewinn würde die höher auflösende Karte einem nur bringen, wenn man Kalibrierungswerte in der Karte ablegen könnte.
Doch zurück zu der Tatsache, dass einige Hersteller nicht den gesamten möglichen Bereich für die Darstellung des Nennbereiches nutzen. Soweit dieser Bereich nicht zu sehr eingeschränkt wird hat dies, wie eben demonstriert, keine spürbare Auswirkung auf die Genauigkeit der Messung.
Um zu verstehen, warum die Hersteller dies machen muss man zunächst die Variante betrachten bei der der gesamte Bereich der Digits (z.B. bei 12 Bit Auflösung) für die Darstellung des Nennbereiches (z.B. 0-10V) verwendet wird. Bei einer Auflösung von 12 Bit würde bei 10,0V der Eingangswert des digitalisierten Analogsignals 2047Dez betragen. Der maximale Wert beträgt "nur" 2047 und nicht, was zu erwarten wäre 4095, weil bei Karten/Modulen, die nur positive Werte messen, auch Integerzahlen mit Vorzeichen verwendet werden und der negative Bereich dadurch wegfällt. Doch was würde passieren, wenn nun stattdessen 10,1V oder gar 10,5V anliegen würden? Die einfache Antwort hierauf lautet, nichts, der Eingangswert beträgt weiterhin 2047Dez, eventuell meldet die Karte über ein Statusbit noch, dass eine Messbereichsüberschreitung vorliegt, aber genaueres kann man nicht mehr erfahren.
Begrenzt der Hersteller jedoch den Bereich der für die Darstellung des Nennbereiches zur Verfügung steht, kann neben der Info das der Messbereich überschritten wurde, im gewissen Rahmen, auch trotz Überschreitung des Nennbereiches noch die Höhe der anliegenden physikalischen Größe ermittelt werden. Da die Karte die angegebene Genauigkeit nur über Ihren Nennbereich erreicht handelt es sich allerdings eher um einen Schätzwert.
Eine Karte die diese Funktionalität bietet ist zum Beispiel die EL3161 von Beckhoff, bei Beckhoff wird diese Funktionalität "Extended range" genannt. Die EL3161 hat einen Nennbereich von 0-10V und bietet eine echte (Werte werden nicht hochskaliert) Auflösung von 16 Bit. Soweit die "Extended Range" Funktionalität aktiviert ist, hat diese Karte neben dem Nennbereich noch einen zweiten, die sogenannte "Overrange Area". Beide Bereiche zusammen bilden einen von Beckhoff "Technical Range" genannten Bereich, der den Nennbereich um ca. 7% überschreitet. Bei 15 Bit wäre der Maximalwert der Digits für den Messbereichsendwert (hier 10V) eigentlich 7FFFHex (32767Dez), bei aktivierter "Extended Range" Funktionalität geht dieser jedoch "nur" bis zu dem Wert 7736Hex (30517Dez), der Bereich von 7737Hex (30518Dez) bis 7FFFHex (32767Dez) ist dann das "Overrange Area". Liegt die Eingangsspannung bei kleiner gleich -0,1V gibt die Karte einen sogenannten Range error aus. Bei Karten die auch negative Werte messen können gibt es diese Funktionalität natürlich auch in negative Richtung.
Bei Siemens ist dieser Ünter- und Übersteuerungsbereich übrigens immer aktiv. Hier gibt es z.B. bei den Karten für die S7-1500er Reihe insgesamt fünf Bereiche, auch wenn der Messbereich lediglich in positive Richtung verläuft (z.B. 0-20mA). Neben dem schon öfters erwähnten Nennbereich (0-20mA, -10-10V, usw.) gibt es in positive Richtung den Übersteuerungsbereich und in negative Richtung den Untersteuerungsbereich und an deren jeweiligen Ende noch den Über-, bzw. Unterlauf. Bei einem Nennbereich von 0-20mA geht der Nennbereich von 0Dez bis 27648Dez (0-20mA) und der Übersteuerungsbereich geht von 27649Dez bis 32511Dez (Bis 23,52mA). Der Wert des Überlaufs beträgt 32767Dez und wird bei Strömen über 23,52mA gemeldet. Der Untersteuerungsbereich geht von -1Dez bis -4864Dez (Bis -3,52mA) und der Unterlauf hat den Wert von -32768 bei Strömen unter -3,52mA.
Neben dem Messwert stellen die analogen Eingangskarten auch Statusbits/-werte zur Verfügung, dabei gibt es verschiedene Möglichkeiten wo diese bereitgestellt werden. Die einfachste Art dabei ist, wenn der Hersteller dafür eigene Objekte verwendet, Es gibt aber auch Hersteller, die die Statusinformationen mit in den Messwert verpacken. Dies funktioniert dann, wenn die Auflösung des Messbereichs kleiner ist als der Speicherbereich in dem er abgelegt wird. Wenn zum Beispiel der Messbereich mit 12 Bit aufgelöst wird und der Bereich in der Karte für den Messwert 16 Bit groß ist, würden noch 4 Bits für Statusinformationen zur Verfügung stehen. Hier würde der Messwert dann um vier Bits nach links geschoben und die dadurch freiwerdenden drei niederwertigen Bits stehen dann für die Statusinformationen zur Verfügung.
Jetzt stellt sich allerdings die Frage, was man anstellen muss um die Statusbit wieder zu entfernen und so nur noch den Messwert zu haben? Im einfachsten Fall lautet die Antwort nichts, man lässt die Statusbits einfach drin und lebt mit der dadurch auftretenden Ungenauigkeit, die soweit der sonstige Messfehler der Karte nicht extrem niedrig ist kaum ins Gewicht fällt. Die in diesem Fall zu verwendende Formel ist dieselbe, wie für Berechnungen mit einer Analogkarte die dieselbe Auflösung hat wie der Messwert dieser Karte plus die Statusbits. Wenn der Messwert der Karte, wie oben angenommen, mit 12 Bit aufgelöst wird und es zusätzlich 4 Statusbits gäbe, würde die Formel genommen werden, die sonst für eine Karte mit 16 Bit Auflösung verwendet wird.

 

[oliver.tonn]

Bei einem Messbereich von 0-10V sähe dann die Formel so aus:



Wenn man die Statusbits gerne entfernt haben möchte, geht dies relativ einfach indem man sie ausmaskiert. Dies funktioniert, indem man eine UND-Verknüpfung mit dem Messwert und FFF0Hex durchführt. In binärer Schreibweise wird der Wert FFF0Hex als 1111 1111 1111 0000 dargestellt. Man kann erkennen, dass die unteren vier Bits nicht gesetzt sind und dadurch diese durch die UND-Verknüpfung im Ergebnis auf 0 gesetzt werden. Nun kann man den so erhaltenen Wert wieder in der Formel verwenden. Auch bei dieser Formel gehe ich wieder von einem Messbereich von 0-10V aus, diese sieht wie folgt aus:



Der Eine oder Andere wird sich jetzt vielleicht wundern, warum ich in der Formel im Nenner die Zahl 32752 als Maximum für die Digits eingesetzt habe und nicht 2047, obwohl die Auflösung des Messwertes ja 12 Bit beträgt. Dies begründet sich durch den Umstand, dass der Messwert um vier Bits nach links verschoben ist, um Platz für die Statusbits zu schaffen. Jedes bitweise Verschieben eines Wertes nach links entspricht einer Multiplikation mit 2, bei einer Verschiebung nach links um vier Bits ergibt dies also Messwert * 2 * 2 * 2 * 2 und das Selbe gilt dann natürlich auch für den Maximalwert der Digits, also 2047 * 2 * 2 * 2 * 2 = 32752.
Die Vorgehensweise mit dem Ausmaskieren funktioniert sowohl bei positiven als auch bei negativen Digits. Die Werte ohne ausmaskierte Statusbits entsprechen dann denen mit ausmaskierten Statusbits, wenn alle Statusbits gesetzt wären, von geringen Rundungsdifferenzen einmal abgesehen. Sind nicht alle Statusbits gesetzt ist der errechnete Wert kleiner als der tatsächliche. Bei einem Messbereich von 0-10V oder (-10V)-10V beträgt der maximale Messfehler, wenn kein Statusbit gesetzt wäre, bei einer Messwertauflösung von 12 Bit und vier Statusbits gegenüber der Methode mit ausgefilterten Statusbits ca. 4,6mV was man in den meisten Fällen vernachlässigen kann. Bei einem Messbereich von 0-20mA beträgt der maximale Messfehler ca. 9.16µA.
Hier nun noch, wie angekündigt, die Beschreibung, was bei Beckhoff anders ist. Durch das Hochskalieren werden ja die untersten Bits nicht genutzt, wenn also um 4 Bits hochskaliert wurde müssten dieuntersten vier Bits immer 0 oder FALSE sein. Bei Beckhoff ist die jedoch nicht so, das liegt daran, dass bei Beckhoff auf den Messwert unter anderem Filterfunktionen angewandt werden.

 

[oliver.tonn]

Zuviel Werbung?
-> Hier kostenlos registrieren

Umsetzung von Skalierungen in SPS-Programme
Der nächste Abschnitt beschäftigt sich damit, wie die gewonnenen Erkenntnisse in Programme umgesetzt werden können. Wobei hier lediglich mit Strukturierten Text (Wird im Folgenden mit ST abgekürzt) gearbeitet wird.
Auf den ersten Blick scheint die Sache ganz einfach zu sein, man muss lediglich die Formeln umsetzen. Die folgende Formel



könnte man in ST z.B. so umsetzen.

r32_Spannung = i16_Messwert * 10 / 32767;

Allerdings ist es nicht so einfach, denn es gibt hierbei einen erheblichen Stolperstein, nämlich das die Steuerung unter bestimmten Umständen nicht mit Fließkommazahlen, sondern mit Ganzzahlen rechnet. Bei einer Rechnung rein mit Ganzzahlen ist das Ergebnis auch bei einer Division immer eine Ganzzahl, auch wenn das Ergebnis, wie in obigem Beispiel, am Ende in einer Fließkommavariable (Stichwort: implizite Typkonvertierung) gespeichert wird.
Durch die Deklaration einer Variable weiß die SPS im wahrsten Sinn des Wortes womit sie rechnen muss, bei direkt im Code angegebenen Werten ist dies jedoch nicht so und die SPS oder genauer die Entwicklungsumgebung muss da sozusagen raten.
Sowohl beim TIA-Portal von Siemens, als auch bei Entwicklungsumgebungen die auf Codesys basieren betrachtet die Entwicklungsumgebung Zahlen ohne Nachkommastellen als Ganzzahl und welche mit als Fließkommazahlen. Möchte man also, dass die Entwicklungsumgebung eine glatte Zahl als Fließkommazahl betrachtet muss man diese mit mindestens einer Nachkommastelle angeben. Möchte man z.B. die Zahl 40 im Code angeben und soll diese als Fließkommazahl interpretiert werden, muss man stattdessen 40.0 eingeben.
Variablen können automatisch über die explizite Typkonvertierung in andere Typen gewandelt werden, da es hier auch zu Problemen kommen kann wäre es allerdings besser dafür, soweit vorhanden, spezielle Funktionen zu nutzen. Sowohl bei Siemens als auch bei Codesys basierten Steuerungen haben diese Funktionen die Namenskonvention QUELLTYP_TO_ZIELTYP. Die Funktion um einen Integerwert in ein Real zu wandeln würde also INT_TO_REAL heißen.
Werden diese Hinweise nicht beachtet, kann es zu erheblichen Rechenfehlern kommen, wie ich noch demonstrieren werde.
Sowohl die Entwicklungsumgebung von Siemens als auch die der Codesys Derivate unterscheiden nicht nur zwischen Fließkomma- und Ganzzahlen aufgrund des Aufbaus der Zahl im Code, sondern stellen beim Übersetzen des Programms auch die Größe der jeweiligen Zahl fest und wählen für diese dann den passenden Typ. Steht im Code z.B. die Zahl 1000 wird hierfür UINT als Typ genutzt, bei -1000 entsprechend INT, bei einer 100000 würde als Typ UDINT genutzt werden. Lediglich bei der Wahl des Typs zur Ablage des Ergebnisses unterscheiden sich die beiden Systeme. Als Typ für das Ergebnis einer Rechnung wird bei Siemens dabei der Typ der Variable genommen die an dem jeweiligen Teil der Rechnung beteiligt ist, ist diese vom Typ INT ist das Ergebnis auch vom Typ INT. Bei Codesys basierten Entwicklungsumgebungen wird für das Ergebnis immer die größte Variante des jeweiligen Typs gewählt, bei Integer-Werten wäre das LINT.
An einem Beispiel das auf obiger Formel basiert soll hier aufgezeigt werden was für ein Ergebnis beim jeweiligen System herauskommt.
Der Wert der Variable i16_Messwert beträgt in diesem Beispiel 9000. Als Ergebnis würde man einen Wert von rund 2,75 mit einem Taschenrechner erhalten. Die Siemens CPU ermittelt jedoch ein Ergebnis von 0 und bei der Beckhoff CPU kommt ein Wert von 2,0 raus. Was lief hier jetzt schief?
Betrachten wir zunächst die Siemens-Seite. Als erstes wird der Messwert mit 10 multipliziert, wie erwähnt nimmt Siemens für die Speicherung des Ergebnisses den Typ der bei der Berechnung beteiligten Variable, in diesem Falle also INT. Hier kommt es nun schon zum ersten Fehler, 9000 * 10 würde als Ergebnis 90000 ergeben, was den Bereich eines INTs (32767) überschreitet, dadurch kommt es zum Überlauf und das errechnete Ergebnis beträgt stattdessen 24464. Dieses (falsche) Ergebnis wird nun durch 32767 geteilt, was ein Ergebnis eigentlich von <1 zur Folge hätte. Da das Ergebnis aber wieder eine Ganzzahl ist gehen die Nachkommastellen sozusagen verloren und das Ergebnis ist 0. Anschließend wird das Ergebnis aufgrund der oben erwähnten impliziten Typkonvertierung zwar in eine Fließkommazahl gewandelt, aber auch dadurch kann nichts anderes als 0 herauskommen.
Da bei Beckhoff für das Zwischenergebnis immer die Variante mit dem größten Bereich eines Typs genommen wird kommt es bei der ersten Rechnung nicht zu einem Überlauf und zumindest das Zwischenergebnis (90000) stimmt hier noch, bei der anschließenden Division kommt es allerdings zum selben Problem wie bei Siemens. Die Rechnung 90000 / 32767 müsste ja eigentlich, wie oben erwähnt, ein Ergebnis von rund 2,75 ergeben, dadurch das das Ergebnis auch eine Ganzzahl ist, gehen auch hier die Nachkommastellen verloren und es bleibt 2 über, die dann durch die implizite Typkonvertierung in einer Fließkommavariable gespeichert wird.
Hier mal ein Einzeiler, der richtig rechnet:

#r32_Drehzahl := INT_TO_REAL(#i16_Messwert) * 1000.0 / 32767.0;

 

[oliver.tonn]

Tipps für Steuerungen ohne Fließkomma Unterstützung
Als letztes kommen nun ein paar Tipps wie man bei Steuerungen vorgehen kann, die keine Fließkommazahlen verarbeiten können. Auch mit diesen Steuerungen kann man Skalierungen durchführen, muss mit Tricks jedoch dafür sorgen, dass alles vor dem Komma stattfindet.
Bei den folgenden Tipps nehme ich eine Steuerung an, die maximal ein UINT verarbeiten kann und für Analogwerte als Maximalwert 1023 ausgibt, gemessen werden soll ein Wert von 0-10V. Im ersten Beispiel soll einfach die aktuell anliegende Spannung ermittelt werden. Normalerweise würde die Formel hierfür wie folgt aussehen:



Nur wird es bei Verwendung dieser Formel bei einer Steuerung ohne Fließkommazahlen in gewissen Situationen zu ziemlichen Ungenauigkeiten kommen.
Angenommen es würde ein Wert von 256Dez vom analogen Eingang gemessen werden. Eine Steuerung die Fließkommazahlen verarbeiten kann würde mit obiger Formel eine Spannung von ca. 2,50V errechnen, ohne diese Fähigkeit käme jedoch eine Spannung von 2V heraus.
Um hier eine gewisse Genauigkeit zu erhalten kann man folgenden Trick anwenden.
Die Steuerung kann ja ein UINT verarbeiten das einen maximalen Wert von 65535 haben kann. Diesen Umstand kann man nutzen um den Wert von 10(V) soweit zu vergrößern, dass der mögliche Bereich der Variable so weit wie möglich ausgenutzt wird. Hierbei muss jedoch beachtet werden, dass bei den folgenden Berechnungen immer nur Ganzzahlen verwendet werden dürfen. Aus diesem Grund wäre, wie später noch klar wird, eine Multiplikation der 10(V) mit 6500 nicht sinnvoll.
Im Gegensatz zur obigen Formel darf man allerdings als nächstes diesen Wert nicht mit dem gemessenen Wert (256) multiplizieren, denn dann käme es zu einem Überlauf, sondern muss diesen erst durch 1023 teilen. Anschließend kann man dieses Ergebnis dann mit dem Messwert multiplizieren. Bei diesem Beispiel käme als Ergebnis 14848 heraus.
Zu Beginn dieses Beispiels wurden die 10(V) ja mit 6000 multipliziert, würde man jetzt das Ergebnis einfach durch 6000 teilen hätte man nichts gewonnen, denn man würde wieder 2V herausbekommen. Stattdessen errechnet man nun die Eingangsspannung nicht in Volt, sondern in mV, dies wird durch eine Division durch 6 erreicht. Das Ergebnis ist dann 2474, was den tatsächlich anliegenden 2500mV schon deutlich näherkommt. Hier sollte jetzt auch klargeworden sein, warum eine Multiplikation der 10(V) mit 6.500 nicht sinnvoll wäre, denn dann hätte man das Ergebnis durch 6,5 teilen müssen, was ja mangels Fließkommafunktionalität nicht möglich ist. Hier noch die entsprechende Formel:



Beim nächsten Beispiel entsprechen die 0-10V einer Zeit von 1-120 Sekunden. Auch hier wird der Bereich der physikalischen Größe (120s - 1s = 119s) zunächst multipliziert, in diesem Fall mit 500 und anschließend auch durch 1023 dividiert. Das Ergebnis wird dann mit dem Messwert multipliziert, durch 5 dividiert und anschließend noch 100 als Offset addiert, dadurch erhält man ein Ergebnis in 1/100s. Hier die passende Formel dazu: