TIA Prüfstand - dynamische Last v2

[ZottelMD]

Hallo Leute,

gleich zu Beginn: dieses Thema schließt gewissermaßen an dieses Thema hier im Forum an https://www.sps-forum.de/sonstige-s...uefstand-drehzahlabhaengiges-gegenmoment.html . Da es thematisch aber doch in eine etwas andere Richtung gehen wird und die langen Ausführungen vom zitierten Thread nicht abschrecken sollen, muss ich ein neues Thema eröffnen.

Ich war sofort begeistert von Holzmichl's Tipps und habe versucht die umzusetzen, doch das alles führte auch zu keine stabilen Prüffahrten (vgl. Link oben). Nun benötige ich einen Regelungstechnischen Ansatz und hoffe, dass mir einer von euch weiterhelfen kann.

Mein Aufbau des "Leistungsprüfstandes" ist folgender:


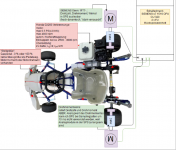
Das vorhandene Gokart wird mit abmontierten Rädern zwischen zwei SIEMENS Servos platziert und die Servos sollen ...
- im Idealfall die Trägheit einer großen, schweren Rolle simulieren können, als würde man sich auf einem Rollenprüfstand bewegen. Dort wird die gesamte vom Antriebsmotor (hier Verbrenner) verfügbare Leistungs zur BEschleunigungs von Massen ja dafür genutzt, um die große schwere Rolle mit gewissem J rotatorisch zu beschleunigen.
- im Idealfall eine gleichmäßig smoothe dynamische Last "simulieren", was eigentlich das gleiche ist, wie der erste Stichpunkt, nur dass man z. B. die Trägheit der simulierten Rolle "umstellen" kann

Zum thematischen Einstieg für alle nicht Antriebstechniker:



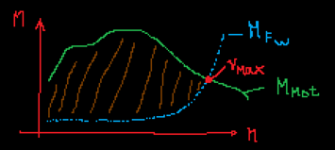
Am Beispiel eines willkürlichen Verbrennungsmotors:
- dem Motor steht über dem Drehzahlband , was er durchfahren kann ein jeweiliges Moment (M) zur Verfügung (Motorkennlinie, grün). Es gibt Bereiche, da hat er viel Moment zur Verfügung und es gibt Bereiche, da kann er weniger.
- das Gegenmoment, was aus Fahrwiderständen resultiert (quasistationäre Reibung, blau) verläuft erst flach und dann steil exponentiell anwachsend (mit hohen Geschwindigkeiten). Hier kommen Rollwiderstand, Lagerreibung, Steigungswiderstand, Windwiderstand zusammen.
- im Schnittpunkt zwischen quasistationären Reibungen und Motorkennlinie ergibt sich v_max (roter Punkt), die Maximalgeschwindigkeit. Bei höheren Geschwindigkeiten steht dem Motor nicht mehr genügend Moment zur Verfügung, um die Widerstände zu überwinden. Er kann nicht schneller werden.
- somit ergibt sich stets aus dem Zwischenbereich zwischen Motorkennlinie (grün) und Lastmomentkennlinie (blau) ein Bereich, ein Reservoir (braun), welches der Motor automatisch nutzt, um rotierende Massen und translatorische Massen zu beschleunigen. Dies ist entsprechend der SKizze über dem gesamten Drehzahlbereich natürlich variabel.

Beispiel:
Auf einem Rollenprüfstand werden die Fahrwiderstände durch die angeschlossene Wirbelstrombremse simuliert (z. B.), die wird bei hohen Drehzahlen mehr "zupacken" als bei niedrigen. Der braune Bereich im Diagramm wird aber automatisch genutzt, um z. B. eine große schwere Rolle mit konstantem Trägheitsmoment zu beschleunigen

M=J*α

. Auch hier ergeben sich somit Drehzahl bereiche, in denen gewisse Drehzahlbereiche schneller (hohes α) oder langsamer (niedriges α) durchlaufen werden.

Dieses Verhalten will ich / muss ich auch auf meinemn Radnaben-Prüfstand nachstellen.

Was ich bisher versucht habe:

1. diskrete Leistungsmessung

Ich habe als absolute Notlösung in meiner SPS programmiert, dass ich im Kart, auf dem Prüfstand sitze und mit F-Tasten das Lastmoment, was statisch von den Servos generiert wird erhöhen kann. Schematisch sieht das so aus:



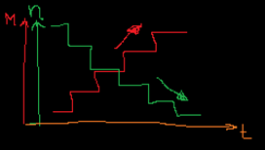
Ich betätige das Gaspedal voll (100 %), die Drehzahl geht auf abgeriegelter MAximaldrehzahl. Dann erhöhe ich nach und nach die Last, z. B. in 5 Nm Schritten, halte die jeweilige "Treppenstufe" für 3 s und bilde den Mittelwert aus Moment und Drehzahl. Der Messpunkt wird gespeichert. Dann zum Nächsten. In Folge dieser Messung wird der Antriebsmotor trotz Vollgas nach und nach bis zum Fast-Stillstand gebremst und die Messung ist beendet.
Was bringt mir das?
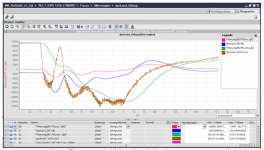
Auf diese Weise, da die Drehzahl nichtlinear sinkt, bei dieser Messung, kann man den Punkt der maximalen Leistung ermitteln

P=M*ω=M*2*π*n

. An der Hinterachse (im eingekuppelten Betrieb Motordrehzahl / 5 geteilt) ergibt sich:

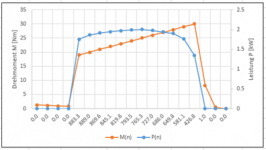
(Achtung Liniendiagramm == nbicht skallierte x-Achse !!)

Für den Drehzahl Verlauf bedeutet das über äquidistante Zeitschritte x[k] = 0, T, 2*T, 3*T ... usw. abgetragen:

 

[ZottelMD]

... und für das Drehmoment bedeutet das:

... und somit bedeutet das für die Leistung (Produkt der beiden) über die jeweilige Drehzahl, bei der das Produkt gebildet wurde, abgetragen:

(Achtung hier wurde wieder die die Hinterachsdrehzahl wieder * 5 multipliziert, um die Motordrehzahl darzustellen)

Problem:

Somit kann ich der Gesamtmessung entnehmen bei welcher Drehzahl die maximale Leistung zu erwarten ist. Das deckt sich dann mit den Literaturangaben oder Überlegungen, die sich aus dem HONDA GX200 Motor-Datenblatt ergeben, ABER ....
Ich bin so nicht in der Lage die Motorkennlinie aufzunehmen, bzw die "Motor-Kennlinie" aufzunehmen, die an der Hinterachse nach den Getriebeverlusten noch sichtbar wird aufzunehmen. Und das ist ja das eigentliche Ziel eines Leistungsprüfstandes. Man möchte die Leistung (Drehmoment und Drehzahl) an der Hinterachse messen (=ca. Radleistung) und zusammen mit der Schleppleistung, die man ermittelt auf die Motorleistung schließen.

Eine M-n-Kennlinie mit der Motorcharakteristik kann ich so nicht messen.

2. Versuch dynamische Leistungsmessung

Die Grundüberlegung, um das Verhalten auf einem Rollenprüfstand nachzuahmen war folgende:
- Drehzahl an der Hinterachse messen
- Drehzahl glätten, weil jede Kolbenexplosion erhebliches "Rauschen" (systematische Störung) verursacht. Gewähltes Filter (aufgrund der Glättung und der Schnelligkeit): "PT2-Filter".
- Differenzenquotient bilden und "momentane" Beschleunigung ausrechnen
- Ergebnis des DiffQuo wieder glätten
- mit dem so gewonnenen Beschleunigungswert in die Gleichung für den Beschleunigungswiderstand bei Bewegung gehen und das theoretisch wirksame Gegenmoment ausrechnen, was bei der momentan gemessenen Beschleunigung herrschen müsste, wenn man draußen auf der Straße fahren würde:

M_B = m_transl.*a_transl.*r_Rad + J_rot.*α_rot = (m*r^2+J)*α

- mit dem berechneten Gegenmoment den Servos sagen: "Jungs: SOLL-Drehzahl 0 rpm (entgegen der euch aufgezwungenen Bewegung durch den HONDA GX200) und dafür dürft ihr XYZ Nm Moment benutzen". Das für die Servos verfügbare Drehmoment wird also "dynamisch" begrenzt (MC_TorqueLimitting-Baustein bei SIEMENS). Zur Laufzeit wird also immer wieder die momentane Beschleunigung ermittelt, das momentane, daraus resultierende Beschleunigungsmoment errechnet und dieses dann auf die Servos aufgeteilt und damit ihr Drehmoment begrenzt, was sie der rotatorischen Bewegung entgegensetzen

Bsp.:
Beschleunigt das Kart also gerade, in einem Zeitpunkt mit z. B. α=450 rpm/s, hat eine Masse von m=80+80 kg (Fahrer & Kart), einen Reifenradius von r=0.131 m und eine auf die Hinterachse reduzierte Drehträgheit von z.B. J=1 kgm², dann ergibt sich ein Gegenmoment, was draußen auf der Straße herrschen würde und dieser Beschleunigung entgegenwirkt von:

M_B = ((80+80) kg * 0.131² m² + 1 kgm² ) * 450 1/(min*s)*1/60 min/s *2*π = 176.51 Nm

Das bedeutet man müsste mit jedem Servo in diesem Moment ca. 88 Nm erzeugen, um die Straßenfahrt zu simulieren. Das ganze reduziert sich aber noch bisschen, weil der Großteil der drehenden Massen ja auch auf dem Prüfstand schon beschleunigt wird und im Grunde "nur" die Räder mit der Rechnung zu simulieren sind. Abgesehen davon müsste man noch die rotierenden Massen der Servomotoren selbst davon abziehen, weil diese auf dem Prüfstand beschleunigt werden, aber draußen eben nicht. Aber das alles ist dann Detailrechnung, die hier jetzt erst einmal nicht weltbewegend sein soll. Fakt ist, selbst wenn ich dregressiv anfange und sage, ich möcht nur und ausschließlich erst einmal 40 Kg translatorische Masse simulieren, um das Verfahren zu testen, führt das nicht zum erhofften Ergebnis, die Radleistung dynamisch zu messen.

Es äußerst sich in Verläufen wie diese:

Trace in TIA: die braune Kurve ist die Hinterachsdrehzahl in [°/s] (negativ, weil Drehrichtung). Grün ist die gefilterte Drehzahl (hier exemplarisch mit starker Glättung). Rot die daraus resultierende Beschleunigung und blau das wiederum daraus resultierende Gegenmoment.

Es zeigt sich, dass das System so nicht funktionieren kann. Es wird das Henne-Ei-Problem deutlich. Die Eingangsgröße ist wieder die Sprungfunktion des Gaspedals. Das soll auch immer so bleiben. Ich möchte zunächst immer nur die Maximalbeschleunigungskennlinien erfassen. Also der Fahrer tritt, wie draußen, auf's Vollgas (0 % -> 100 %). Auf dem Prüfstand erzeugt das zunächst einen hohen Drehzahlanstieg. Damit wird eine hohe Beschleunigung ermittelt, die zeitlich versetzt zu einer hohen Last führt. Dann bricht die Drehzahl ein, die Last wird geringer und alles wieder von vorn.

Die Graphen, wenn man nicht, ein ultraverzögerndes Filter einsetzt, sehen noch viel krasser und schwingender aus. Hierbei zeig ich euch mit der letzten Abb. erst einmal nur den qualitaitiven Verlauf. Auf jeden Fall funktioniert das Gedachte, um die dynamische Leistungsmessung durchzuführen nicht. Ganz und Gar nicht.

Woran könnte das liegen?

Ich erkläre es mir, so, dass ich damit im Grunde keine Regleung darstelle, auch wenn innerhalb der SPS und Antriebstechnik (CU, FU etc.) Regelung stattfinden. Aber global betrachtet, erfasse ich mit dieser Messung ja die momentane Drehzahl an der Hinterachse. Dann berechne ich die Last, was im diskreten automatisch immer mit zeitlicher Verzögerung verbunden ist und dann stelle ich die Drehmomentbegrenzung ein/nach. In meinen Augen, auch wenn es in meinem Kopf funktionieren müsste, ist das eine Steuerung und keine Regelung. Ich führe nirgends eine Messgröße zurück. Ich sage den Servos die ganze Zeit SOLL-Drehzahl 0 rpm und dafür dürft ihr das und das Moment nutzen.

Was für Möglichkeiten habe ich?

Ich denke ich habe nicht so viele Möglichkeiten, aber genau da frage ich bei euch um Rat.
Fakt ist:
- ich kann am Kart zunächst keine Live-Daten erfassen, die mit dem SPS-Daten (Messung an der Hinterachse) synchronisiert sind
- das Kart hat kein elektronisches Gaspedal oder elektronische Drosselklappe
- das Kart hat kein Steuergerät
- das Kart hat somit keine Motordrehzahl oder Verebrennungsdruck-Information, die es an eine SPS-Regelung weitergeben kann
- das Kart ist als strunz dumm anzusehen und das einzige, was man misst, ist alles an der Hinterachse

Bei allen Prüfständen, die ich so recherchiere (Bücher & Patente) tritt aber genau das immer wieder auf. Alle Regelungen werden aufgebaut, indem Aktualparameter aus dem Antriebsaggregat erfasst werden und in den Regelkreis mit eingehen.

Beispielsweise Systeme mit Beobachter/Schätzer:

In diesem Realisierungen der Prüfstände werden Aktualparameter wie Drosselklappenstellung, Gas oder Motormoment einem Abschnitt im Regelkreis zugeführt, der aus diesen Werten einen anderen schätzt, eine Vorhersage trifft, z. B. eine Vorhersage für die Drehzahl, die sich an der Hinterachse ergeben müsste, wenn man draußen fahren würde. Dieser geschätzte Wert bildet dann quasi den Sollwert der Regelung und die momentane SErvo-Last wird dahingehend angepasst, dass dieser Verlauf gut eingehalten wird.
Problem: mir ist zusätzlich zu den "Fakt ist"-Nennungen schleierhaft, wie ich daraus die "Motorkennlinie" für maximale Beschleunigung ermitteln kann / soll

Hilfeschrei:

hat jemand von euch eine Idee, wie ich es mit der vorhandenen Technik regelungtechnisch umsetzen könnte eine 2dynamische" Last zu generieren und so eine Radleistung vernüftig zu messen, als würde man draußen auf der Straße fahren?

Was ich anbieten kann:
Durch verbaute unabhängige Messtechnik an der Hinterachse eines Verbrennerkarts, bin ich in der Lage, "den Fahrzyklus" draußen auf der Straße aufzunehmen. Ich habe Dehnungmessstreifen auf der Hinterachse verbaut und einen Hallsensor, der 1 Imp/rot liefert. Das ganze erfolgt mit Funk-Messtechnik von Microstrain. Durch POST-Processing kann ich dann analysieren, was ich draußen auf der Straße "geleistet" habe:



Der grün-blaue Zuckerhut ist eine aus dem Stand-Maximalbeschleunigung mit gefolgter aktiver Bremsung. orange-lila zittrige Schlange ist das dabei festgestellte Drehmoment auf der Hinterachse (Dehnungmesstsreifen). Filtere, glätte und bearbveite ich diese Messdaten in MATLAB erhalte ich ungefähr eine Radleistungkennlinie, die qualitativ so aussieht:



Drehmomentüberhöhung bei niedrigen Hinterachsdrehzahlen. Das kommt durch den "schlagartigen" Eingriff der automatischen Fliehkraftkupplung. Die Messtelle des Drehmomentes ist einseitig appliziert. Nimmt man an, dass sich das Beschleunigungmoment auf beide Räder zu gleichen Teilen aufteilt, könnte man für die Maximalleistung bei ca. 3.6 kW liegen, was einen plausiblen Wert ergibt.
Hinweis: Angabe im Datenblatt HONDA GX200
- maximal theoretisch verfügbar 6.5 PS == 4.8 kW
- theoretische Verluste bei Antriebssträngen η = 0.7 ... 0.8 (Zahnräder, Kupplung, Öl etc.)
- 3.6 kW / 4.8 kW = 0.75 -> somit sehe ich die Messergebnisse an der Hinterachse durch nachträgliche MATLAB-Bearbeitung als plausibel an.

Somit habe ich einen Eindruck, wo die Reise auf dem Prüfstand hingehen müsste, als Referenz. Allerdings ist durch die aufwändige Postbearbeitung immer in Frage zu stellen, inwieweit das im Detail der Realität entspricht.
Der Prüfstand soll genau das dann untersuchen. Inwieweit kommen vergleichbare Ergebnisse auf dem Prüfstand raus?

Was ich aber auf jeden Fall so ermitteln kann und habe, ist der Verlauf der Fahrwiderstände (durch Ausrollversuche und vorangeganer aufwändigen Ermittlung vieler/aller Trägheitsmomente). Durch die auf der Hinterachse verbaute Messtechnik und Ausrollversuche kann ich sagen, ein 80 kg Fahrer würde den und den Verlauf der "quasistationären" Fahrwiderstände erzeugen, die dann auf dem Prüfstand simuliert werden können.
Das Problem mit den bis jetzt nicht Realisierbaren dynamischen / Beschleunigungswiderständen bleibt aber omnipresent.

Hat jemand einen geilen regelungstechnischen Ansatz wie ich das angehen kann?

Ich verweise bei Interesse noch auf zusätzliche Literatur, die einschlägig dafür zu sein scheint:
Paulwebers-Buchauszug:

- Paulwebers Buch zu Prüfständen mit gaaaaaanz viel Wissen drum herum:
https://link.springer.com/chapter/10.1007/978-3-658-04453-4_4
!!! das eigentlich für mich RelevanteKapitel ist Kapitel 4.5 (Buchseite 302):

- beispiehafte Patente oder Paper:
Verfahren und Einrichtung zur Regelung einer Prufstandsanordnung
https://patentimages.storage.googleapis.com/9c/fc/8b/24df0d37a568ef/WO2011022746A1.pdf
Umsetzung an einem Beispiel-Kettenfahrzeug:
https://www.researchgate.net/public...cles_Based_on_a_Dynamic_Load_Emulation_Method

Allen ist gemeinsam, dass sie bestimmte Aktualparameter des Antriebes in die Regelung reingeben. Das Einzige, was ich mir vorstellen könnte, wäre, wenn ich hier immer eine Maximalbeschleunigung betrachte, könnte ich eine Sprungfunktion für alpha-SOLL in einen Regelkreis einpflegen und so tun, als käme er von meiner Drosselklappe oder meinem Gaspedal.

Denn sofern ich die und andere Literatur richtig verstehe, fordert man im Grunde mit dem Gaspedal immer nur alpha an. Also ein gewisses Maß an Beschleunigung. Der Verbrennungsmotor setzt die Anfoerung dann um, in dem er entsprechend seines Motordiagrammes, seiner Motorkennlinienschar die nächst gelegende auswählt oder interpoliert und Drehmoment über Drehzahl realisiert, um dieser Anforderung nachzukommen.
So könnte/würde man z. B. einen Verbrenner in MATLAB Simscape/Simulink simulieren. Müsste/sollte ich dann z. B. im Moment, in dem mein Prüfstand eine Drehzahl erhöhung registriert ( da kann ich ja mit Threshold arbeiten), so tun als gäbe ich ein alpha von 100 % in einen Regelkreis rein? Hilft mir das?

Viele hilfesuchende Grüße
Basti